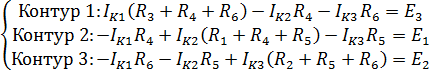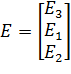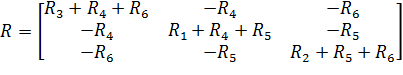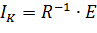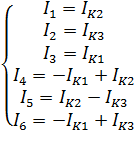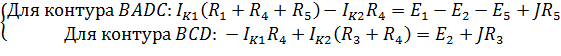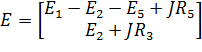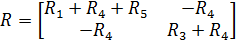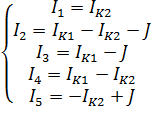Метод контурных токов

  Уравнения Кирхгофа позволяют рассчитать электрическую любую цепь, но при этом число решаемых уравнений может быть велико. Для сокращения числа решаемых уравнений рационализируют составление и решение уравнений Кирхгофа, применяя для расчета метод контурных токов. Метод основан на применении второго закона Кирхгофа и позволяет сократить при расчете сложных систем число решаемых уравнений. Во взаимно независимых контурах, где для каждого контура хотя бы одна ветвь входит только в этот контур, рассматривают условные контурные токи во всех ветвях контура. Контурные токи в отличие от токов ветвей имеют свои индексы и их направление в контуре целесообразно выбирать одинаковым, например, по часовой стрелке. Уравнения составляют по второму закону Кирхгофа для контурных токов. Токи ветвей выражают через контурные токи по первому закону Кирхгофа. Число выбираемых контуров и число решаемых уравнений равно числу уравнений, составляемых по второму закону Кирхгофа. Сумма сопротивлений всех резистивных элементов каждого контура со знаком плюс является коэффициентом при токе контура. Знак коэффициента при токе смежных контуров зависит от совпадения или несовпадения направления смежных контурных токов. ЭДС входит в уравнение со знаком плюс, если направление ЭДС и направление тока контура совпадают.

Рассмотрим пример:

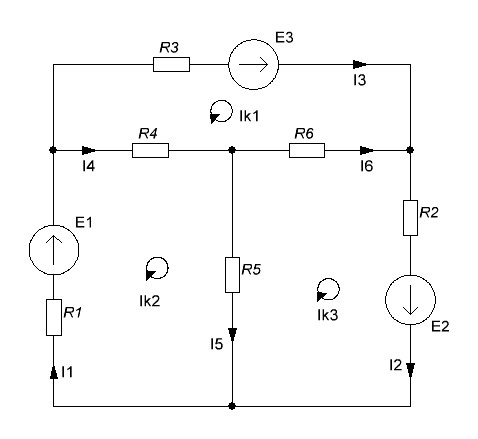
  Для составления системы уравнений по методу контурных токов необходимо определить количество независимых контуров, в данной схеме их три. Положительные направления токов и обходов контура указаны на схеме.
Запишем систему уравнений

  Матрица ЭДС

  Матрица коэффициентов перед токами

  Контурные токи найдем по формуле

  Токи в смежных ветвях ток равны алгебраической сумме контурных токов смежных контуров с учетом их направления

  Реализуем расчёты в систему Matlab

clear
clc

E1 = 10;
E2 = 12;
E3 = 30;
R1 = 9;
R2 = 6;
R3 = 5;
R4 = 8;
R5 = 4;
R6 = 10;

R = [ R3+R4+R6 -R4 -R6
      -R4 R1+R4+R5 -R5
     -R6 -R5 R2+R5+R6 ];
E = [ E3; E1; E2 ];
Ik = inv(R)*E
I1 = Ik(2)
I2 = Ik(3)
I3 = Ik(1)
I4 = -Ik(1)+Ik(2)
I5 = Ik(2)-Ik(3)
I6 = -Ik(1)+Ik(3)

  Были получены следующие результаты. Контурные токи:

Ik =

    3.2291
    2.2124
    2.6571

  Токи в ветвях

I1 =

    2.2124

I2 =

    2.6571

I3 =

    3.2291

I4 =

   -1.0167

I5 =

   -0.4446

I6 =

   -0.5721

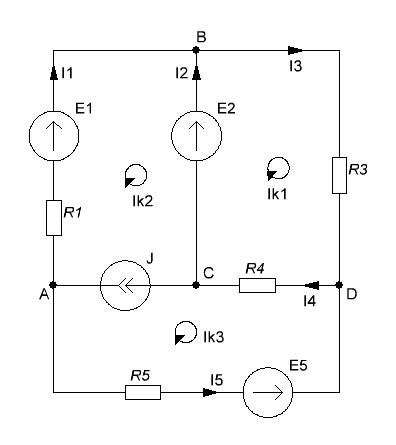
  Отрицательные значения токов говорят о том, что их реальное направление противоположно выбранному.

  Рассмотрим пример для схемы содержащей источник тока:

  В данной схеме три независимых контура. Поскольку в схеме присутствует источник тока, будем считать, что один контурный ток нам известен, поэтому в системе будет 2 уравнения. Запишем систему уравнений для контуров BADC (I_k1) и BCD  (I_k2) , ток контура BCAD (I_k3)  примем равным току источника тока

    Матрица ЭДС

    Матрица коэффициентов перед токами

    Контурные токи найдем по формуле

    Токи в смежных ветвях ток равны алгебраической сумме контурных токов смежных контуров с учетом их направления

  Реализуем расчёты в систему Matlab

clear
clc

R1=60;
R3=60;
R4=60;
R5=60;
E1=60;
E2=90;
E5=30;
J=2;

E = [ E2+J*R3; E1-E2-E5+J*R5 ];
Z = [ R3+R4 -R4
      -R4 R1+R4+R5 ];
Ik = inv(Z)*E
I1 = Ik(2)
I2 = Ik(1)-Ik(2)-J
I3 = Ik(1)-J
I4 = Ik(1)-Ik(2)
I5 = -Ik(2)+J

  Были получены следующие результаты. Контурные токи:

Ik =

    2.3000
    1.1000

  Токи в ветвях

I1 =

    1.1000

I2 =

   -0.8000

I3 =

    0.3000

I4 =

    1.2000

I5 =

    0.9000

  Отрицательные значения токов говорят о том, что их реальное направление противоположно выбранному.