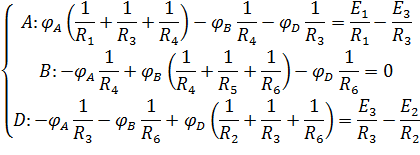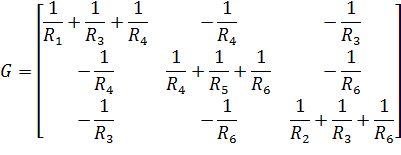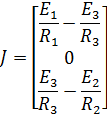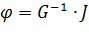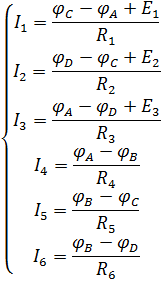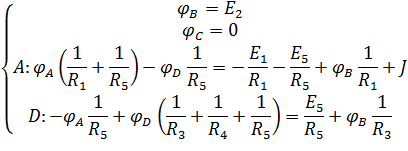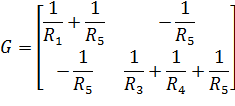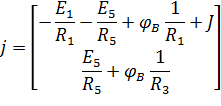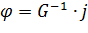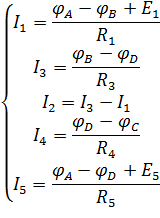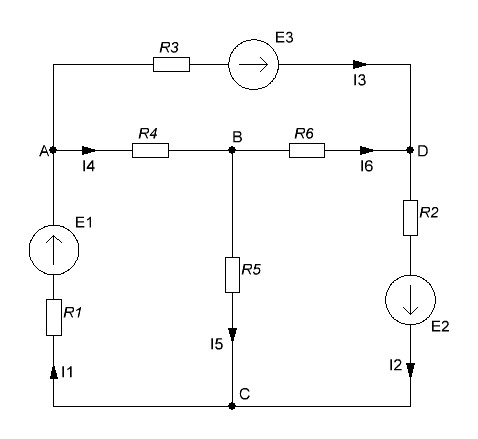
Метод узловых потенциалов

  Метод основан на применении первого закона Кирхгофа и позволяет сократить число решаемых уравнений при нахождении неизвестных токов до "количество узлов"-1. Ток в любой цепи может быть найден по закону Ома для участка цепи, содержащего ЭДС. Для того чтобы можно было применить закон Ома, надо знать потенциалы узлов. Допустим, что в схеме x узлов. Т. к. любая (одна) точка схемы может быть заземлена без изменения токораспределения в схеме, то мы вправе один из узлов схемы мысленно заземлить, т. е. принять потенциал его равным нулю. При этом число неизвестных уравнений уменьшить с x до x-1. Число неизвестных в методе узловых потенциалов равно числу уравнений, которые надо составить для схемы по первому закону Кирхгофа.

  Рассмотрим пример:

  Потенциал узла C примем равным нулю. Запишем систему уравнений

    Матрица проводимостей

    Матрица токов

    Узловые потенциалы определим по формуле

    Определим токи в ветвях

  Реализуем расчёты в системе Matlab:

clear
clc

E1 = 10;
E2 = 12;
E3 = 30;
R1 = 9;
R2 = 6;
R3 = 5;
R4 = 8;
R5 = 4;
R6 = 10;

G = [ 1/R1+1/R3+1/R4 -1/R4 -1/R3
     -1/R4 1/R4+1/R5+1/R6 -1/R6
     -1/R3 -1/R6 1/R2+1/R3+1/R6 ];
J = [ E1/R1-E3/R3; 0; E3/R3-E2/R2 ];
phi = inv(G)*J
phiA = phi(1);
phiB = phi(2);
phiC = 0;
phiD = phi(3);

I1 = (phiC-phiA+E1)/R1
I2 = (phiD-phiC+E2)/R2
I3 = (phiA-phiD+E3)/R3
I4 = (phiA-phiB)/R4
I5 = (phiB-phiC)/R5
I6 = (phiB-phiD)/R6

  Были получены следующие результаты. Узловые потенциалы:

phi =

   -9.9120
   -1.7785
    3.9423

  Токи в ветвях

I1 =

    2.2124

I2 =

    2.6571

I3 =

    3.2291

I4 =

   -1.0167

I5 =

   -0.4446

I6 =

   -0.5721

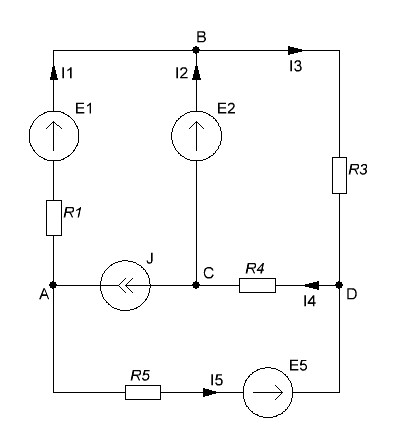
  Отрицательные значения токов говорят о том, что их реальное направление противоположно выбранному.

Рассмотрим пример для цепи с источником тока и ветвью, содержащую только источник ЭДС:

  Потенциал узла C примем равным нулю. Поскольку цепь имеет ветвь содержащую только источник ЭДС, то потенциал узла B будем считать равным напряжению источника ЭДС E₂. Запишем систему уравнений

    Матрица проводимостей

    Матрица токов

    Узловые потенциалы определим по формуле

    Определим токи в ветвях

  Реализуем расчёты в системе Matlab:

clear
clc

R1=60;
R3=60;
R4=60;
R5=60;
E1=60;
E2=90;
E5=30;
J=2;

phiB = E2;
phiC = 0;

j = [ (-E1/R1-E5/R5+phiB/R1+J); (E5/R5+phiB/R3) ];
G = [ 1/R1+1/R5 -1/R5
     -1/R5 1/R3+1/R4+1/R5 ];
phi = inv( G )*j

phiA = phi(1);
phiD = phi(2);

I1 = (phiA-phiB+E1)/R1
I3 = (phiB-phiD)/R3
I4 = (phiD-phiC)/R4
I5 = (phiA-phiD+E5)/R5
I2 = I3-I1

  Были получены следующие результаты. Узловые потенциалы:

phi =

   96.0000
   72.0000

  Токи в ветвях

I1 =

    1.1000

I3 =

    0.3000

I4 =

    1.2000

I5 =

    0.9000

I2 =

   -0.8000

  Отрицательные значения токов говорят о том, что их реальное направление противоположно выбранному.